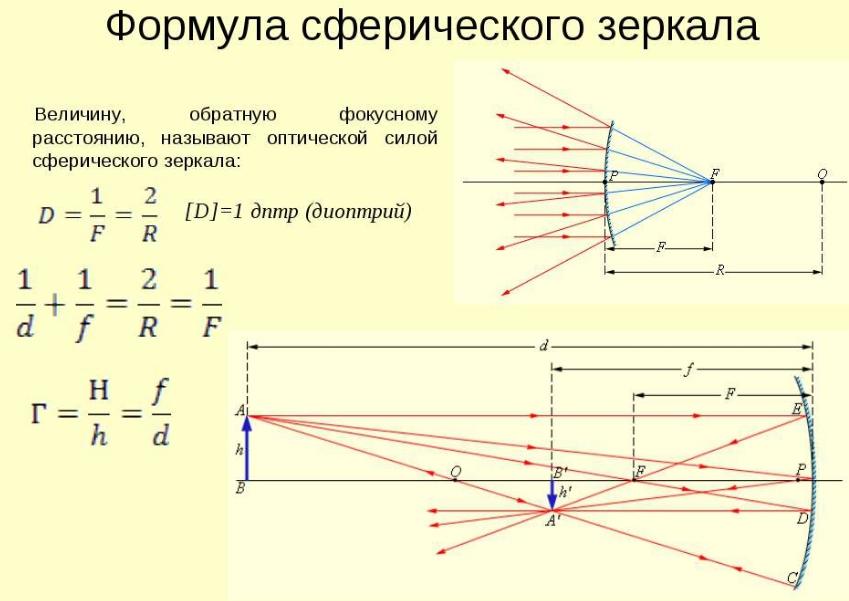
प्रकाश परावर्तन के नियम और उनकी खोज का इतिहास
प्रकाश के परावर्तन के नियम की खोज प्रेक्षणों और प्रयोगों द्वारा की गई थी। बेशक, इसे सैद्धांतिक रूप से प्राप्त किया जा सकता है, लेकिन अब उपयोग किए जाने वाले सभी सिद्धांतों को परिभाषित और व्यवहार में प्रमाणित किया गया है। इस घटना की मुख्य विशेषताओं को जानने से प्रकाश योजना और उपकरण चयन में मदद मिलती है। यह सिद्धांत अन्य क्षेत्रों में भी काम करता है - रेडियो तरंगें, एक्स-रे, आदि। प्रतिबिंब में बिल्कुल वैसा ही व्यवहार करें।
प्रकाश और उसकी किस्मों का प्रतिबिंब क्या है, तंत्र
कानून निम्नानुसार तैयार किया गया है: आपतित और परावर्तित किरणें एक ही तल में होती हैं, जो परावर्तक सतह के लंबवत होती हैं, जो आपतन बिंदु से निकलती हैं। आपतन कोण परावर्तन कोण के बराबर होता है।
संक्षेप में, परावर्तन एक भौतिक प्रक्रिया है जिसमें एक किरण, कण या विकिरण एक विमान के साथ परस्पर क्रिया करते हैं। दो मीडिया की सीमा पर तरंगों की दिशा बदल जाती है, क्योंकि उनके अलग-अलग गुण होते हैं।परावर्तित प्रकाश हमेशा उसी माध्यम में लौटता है जिससे वह आया था। प्राय: परावर्तन के दौरान तरंगों के अपवर्तन की घटना भी देखी जाती है।
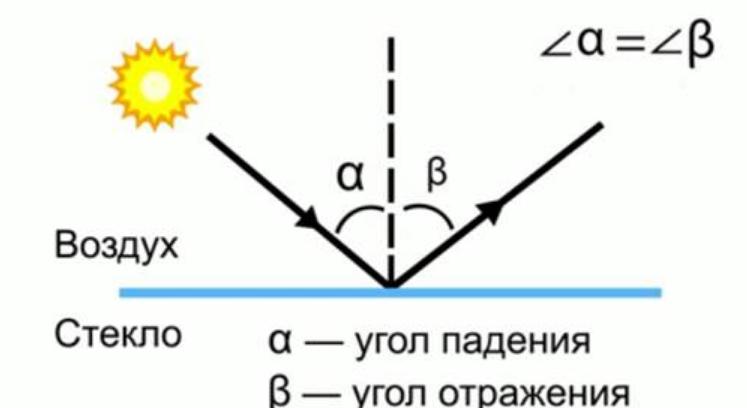
दर्पण प्रतिबिंब
इस मामले में, परावर्तित और आपतित किरणों के बीच एक स्पष्ट संबंध है, यह इस किस्म की मुख्य विशेषता है। मिररिंग के लिए विशिष्ट कई मुख्य बिंदु हैं:
- परावर्तित किरण हमेशा एक समतल में होती है जो आपतित किरण से होकर गुजरती है और अभिलम्ब परावर्तक सतह की ओर होती है, जिसे आपतन बिंदु पर फिर से बनाया जाता है।
- आपतन कोण प्रकाश पुंज के परावर्तन कोण के बराबर होता है।
- परावर्तित बीम की विशेषताएं बीम बीम के ध्रुवीकरण और इसके घटना के कोण के समानुपाती होती हैं। साथ ही, संकेतक दो वातावरणों की विशेषताओं से प्रभावित होता है।
इस मामले में, अपवर्तक सूचकांक विमान के गुणों और प्रकाश की विशेषताओं पर निर्भर करते हैं। यह परावर्तन जहाँ भी चिकनी सतह होती है वहाँ पाया जा सकता है। लेकिन विभिन्न वातावरणों के लिए, स्थितियां और सिद्धांत बदल सकते हैं।
कुल आंतरिक प्रतिबिंब
ध्वनि और विद्युत चुम्बकीय तरंगों के लिए विशिष्ट। उस बिंदु पर होता है जहां दो वातावरण मिलते हैं। इस मामले में, तरंगों को एक ऐसे माध्यम से गिरना चाहिए जिसमें प्रसार वेग कम हो। प्रकाश के संबंध में, हम कह सकते हैं कि इस मामले में अपवर्तनांक बहुत बढ़ जाते हैं।
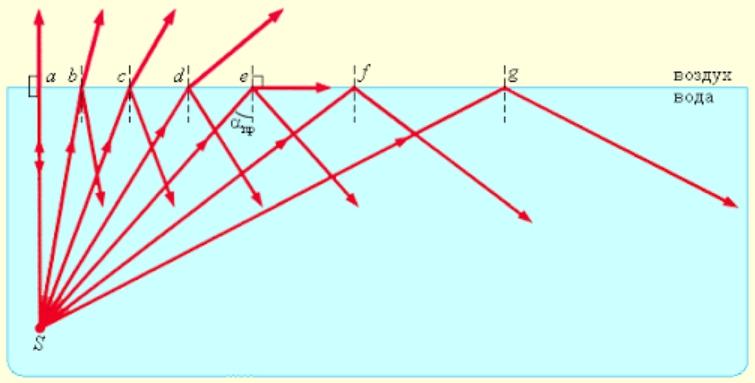
प्रकाश पुंज का आपतन कोण अपवर्तन कोण को प्रभावित करता है। इसके मान में वृद्धि के साथ, परावर्तित किरणों की तीव्रता बढ़ जाती है, और अपवर्तित किरणें घट जाती हैं।जब एक निश्चित महत्वपूर्ण मान तक पहुँच जाता है, तो अपवर्तनांक शून्य हो जाता है, जिससे किरणों का पूर्ण परावर्तन हो जाता है।
महत्वपूर्ण कोण की गणना अलग-अलग मीडिया के लिए अलग-अलग की जाती है।
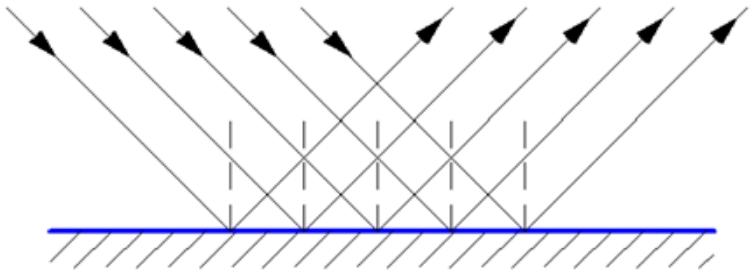
प्रकाश का विसरित परावर्तन
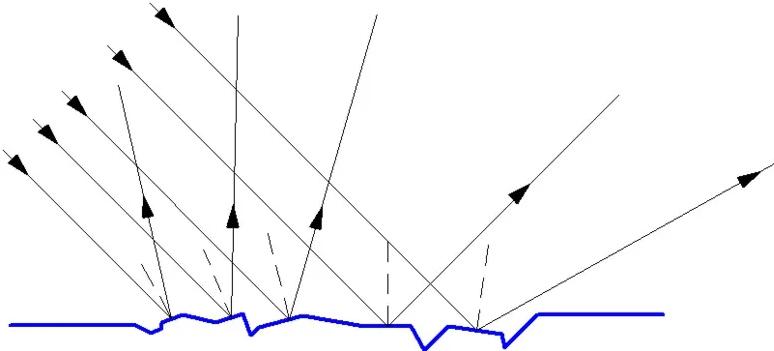
यह विकल्प इस तथ्य की विशेषता है कि जब यह असमान सतह से टकराता है, तो किरणें अलग-अलग दिशाओं में परावर्तित होती हैं। परावर्तित प्रकाश केवल बिखरता है और यह इस वजह से है कि आप अपने प्रतिबिंब को असमान या मैट सतह पर नहीं देख सकते हैं। किरण प्रसार की घटना तब देखी जाती है जब अनियमितताएं तरंग दैर्ध्य के बराबर या उससे अधिक होती हैं।
इस मामले में, एक और एक ही विमान प्रकाश या पराबैंगनी के लिए व्यापक रूप से प्रतिबिंबित हो सकता है, लेकिन साथ ही साथ इन्फ्रारेड स्पेक्ट्रम को अच्छी तरह से प्रतिबिंबित करता है। यह सब तरंगों की विशेषताओं और सतह के गुणों पर निर्भर करता है।
उल्टा प्रतिबिंब
यह घटना तब देखी जाती है जब किरणें, तरंगें या अन्य कण वापस परावर्तित होते हैं, अर्थात स्रोत की ओर। इस संपत्ति का उपयोग खगोल विज्ञान, प्राकृतिक विज्ञान, चिकित्सा, फोटोग्राफी और अन्य क्षेत्रों में किया जा सकता है। दूरबीनों में उत्तल लेंस की व्यवस्था के कारण उन तारों के प्रकाश को देखना संभव है जो नग्न आंखों को दिखाई नहीं देते हैं।
प्रकाश के स्रोत पर लौटने के लिए कुछ शर्तें बनाना महत्वपूर्ण है, यह अक्सर प्रकाशिकी और किरणों की किरण दिशा के माध्यम से प्राप्त किया जाता है। उदाहरण के लिए, इस सिद्धांत का उपयोग अल्ट्रासाउंड अध्ययन में किया जाता है, परावर्तित अल्ट्रासोनिक तरंगों के लिए धन्यवाद, अध्ययन के तहत अंग की एक छवि मॉनिटर पर प्रदर्शित होती है।
परावर्तन के नियमों की खोज का इतिहास
यह घटना लंबे समय से जानी जाती है।पहली बार, प्रकाश के परावर्तन का उल्लेख "काटोप्ट्रिक" कार्य में किया गया था, जो 200 ईसा पूर्व की है। और प्राचीन यूनानी विद्वान यूक्लिड द्वारा लिखित। पहले प्रयोग सरल थे, इसलिए उस समय कोई सैद्धांतिक आधार नहीं दिखाई दिया, लेकिन यह वह था जिसने इस घटना की खोज की थी। इस मामले में, दर्पण सतहों के लिए फर्मेट के सिद्धांत का इस्तेमाल किया गया था।
फ्रेस्नेल सूत्र
अगस्टे फ्रेस्नेल एक फ्रांसीसी भौतिक विज्ञानी थे जिन्होंने कई सूत्र विकसित किए जो आज तक व्यापक रूप से उपयोग किए जाते हैं। इनका उपयोग परावर्तित और अपवर्तित विद्युत चुम्बकीय तरंगों की तीव्रता और आयाम की गणना में किया जाता है। उसी समय, उन्हें अलग-अलग अपवर्तक मूल्यों वाले दो मीडिया के बीच एक स्पष्ट सीमा से गुजरना होगा।
फ्रांसीसी भौतिक विज्ञानी के सूत्रों में फिट होने वाली सभी घटनाओं को फ्रेस्नेल प्रतिबिंब कहा जाता है। लेकिन यह याद रखना चाहिए कि व्युत्पन्न सभी कानून तभी मान्य होते हैं जब मीडिया आइसोट्रोपिक हो, और उनके बीच की सीमा स्पष्ट हो। इस मामले में, आपतन कोण हमेशा परावर्तन कोण के बराबर होता है, और अपवर्तन का मान स्नेल के नियम द्वारा निर्धारित किया जाता है।
यह महत्वपूर्ण है कि जब प्रकाश समतल सतह पर पड़ता है, तो दो प्रकार के ध्रुवीकरण हो सकते हैं:
- पी-ध्रुवीकरण इस तथ्य की विशेषता है कि विद्युत चुम्बकीय क्षेत्र का वेक्टर आपतन के तल में स्थित है।
- एस-ध्रुवीकरण पहले प्रकार से भिन्न होता है जिसमें विद्युत चुम्बकीय तरंग तीव्रता वेक्टर उस विमान के लंबवत स्थित होता है जिसमें घटना और परावर्तित किरण दोनों स्थित होते हैं।

विभिन्न ध्रुवीकरण वाली स्थितियों के लिए सूत्र भिन्न होते हैं।यह इस तथ्य के कारण है कि ध्रुवीकरण बीम की विशेषताओं को प्रभावित करता है और यह विभिन्न तरीकों से परिलक्षित होता है। जब प्रकाश एक निश्चित कोण पर गिरता है, तो परावर्तित किरण पूरी तरह से ध्रुवीकृत हो सकती है। इस कोण को ब्रूस्टर कोण कहा जाता है, यह इंटरफ़ेस पर मीडिया की अपवर्तन विशेषताओं पर निर्भर करता है।
वैसे! परावर्तित किरण हमेशा ध्रुवीकृत होती है, भले ही आपतित प्रकाश अध्रुवित हो।
हाइजेंस सिद्धांत
ह्यूजेंस एक डच भौतिक विज्ञानी हैं जो उन सिद्धांतों को प्राप्त करने में सफल रहे जो किसी भी प्रकृति की तरंगों का वर्णन करना संभव बनाते हैं। यह इसकी मदद से है कि अक्सर वे प्रतिबिंब के कानून और दोनों को साबित करते हैं प्रकाश के अपवर्तन का नियम.
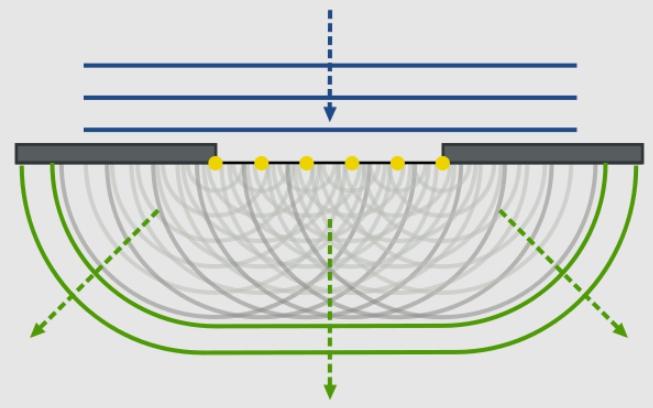
इस मामले में, प्रकाश को एक सपाट आकार की लहर के रूप में समझा जाता है, अर्थात सभी तरंग सतह समतल होती हैं। इस मामले में, तरंग सतह एक ही चरण में दोलनों के साथ बिंदुओं का एक समूह है।
शब्दांकन इस प्रकार है: कोई भी बिंदु जिस पर बाद में विक्षोभ आया है, गोलाकार तरंगों का स्रोत बन जाता है।
वीडियो में, ग्रेड 8 भौतिकी के एक कानून को ग्राफिक्स और एनीमेशन का उपयोग करके बहुत ही सरल शब्दों में समझाया गया है।
फेडोरोव की पारी
इसे फेडोरोव-एम्बर प्रभाव भी कहा जाता है। इस मामले में, पूर्ण आंतरिक परावर्तन के साथ प्रकाश पुंज का विस्थापन होता है। इस मामले में, बदलाव महत्वहीन है, यह हमेशा तरंग दैर्ध्य से कम होता है। इस विस्थापन के कारण, परावर्तित किरण उसी तल में नहीं होती है जिसमें आपतित किरण होती है, जो प्रकाश के परावर्तन के नियम के विरुद्ध जाती है।
वैज्ञानिक खोज के लिए डिप्लोमा एफ.आई. 1980 में फेडोरोव।
1955 में गणितीय गणनाओं की बदौलत एक सोवियत वैज्ञानिक द्वारा किरणों के पार्श्व विस्थापन को सैद्धांतिक रूप से सिद्ध किया गया था। इस आशय की प्रायोगिक पुष्टि के लिए, फ्रांसीसी भौतिक विज्ञानी एम्बर ने इसे थोड़ी देर बाद किया।
व्यवहार में कानून का प्रयोग

विचाराधीन कानून जितना लगता है उससे कहीं अधिक सामान्य है। इस सिद्धांत का व्यापक रूप से विभिन्न क्षेत्रों में उपयोग किया जाता है:
- दर्पण सबसे सरल उदाहरण है। यह एक चिकनी सतह है जो प्रकाश और अन्य प्रकार के विकिरण को अच्छी तरह से दर्शाती है। फ्लैट संस्करण और अन्य आकृतियों के तत्वों दोनों का उपयोग किया जाता है, उदाहरण के लिए, गोलाकार सतह वस्तुओं को दूर ले जाने की अनुमति देती है, जो उन्हें कार में रियर-व्यू मिरर के रूप में अपरिहार्य बनाती है।
- विभिन्न ऑप्टिकल उपकरण विचारों के सिद्धांतों के कारण भी काम करता है। इसमें हर जगह पाए जाने वाले चश्मे से लेकर उत्तल लेंस या दवा और जीव विज्ञान में उपयोग किए जाने वाले सूक्ष्मदर्शी तक सब कुछ शामिल है।
- अल्ट्रासाउंड डिवाइस भी इसी सिद्धांत का प्रयोग करते हैं। अल्ट्रासाउंड उपकरण सटीक परीक्षाओं की अनुमति देता है। एक्स-रे समान सिद्धांतों के अनुसार प्रचारित करते हैं।
- माइक्रोवेव ओवन्स - व्यवहार में प्रश्न में कानून के आवेदन का एक और उदाहरण। इसमें वे सभी उपकरण भी शामिल हैं जो इन्फ्रारेड विकिरण (उदाहरण के लिए, नाइट विजन डिवाइस) के कारण संचालित होते हैं।
- अवतल दर्पण प्रदर्शन बढ़ाने के लिए फ्लैशलाइट और लैंप की अनुमति दें। इस मामले में, प्रकाश बल्ब की शक्ति दर्पण तत्व के उपयोग के बिना बहुत कम हो सकती है।
वैसे! प्रकाश के परावर्तन से हमें चाँद और तारे दिखाई देते हैं।
प्रकाश के परावर्तन का नियम कई प्राकृतिक घटनाओं की व्याख्या करता है, और इसकी विशेषताओं के ज्ञान ने ऐसे उपकरण बनाना संभव बना दिया है जो हमारे समय में व्यापक रूप से उपयोग किए जाते हैं।